A Visualization of Air Pollution Distribution over an Observed Area Surrounded by Mountains: A Computational Approach

Udomsak  RAKWONGWAN; Piyanut  TANGMANUSSUKUM; Sanae  RUJIVAN

doi:10.48048/wjst.2021.9805

Authors

Udomsak RAKWONGWAN Department of Mathematics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand https://orcid.org/0000-0001-6909-4111
Piyanut TANGMANUSSUKUM Division of Mathematics and Statistic, School of Science, Walailak University, Nakhon Si Thammarat 80160, Thailand https://orcid.org/0000-0003-1741-5248
Sanae RUJIVAN Center of Excellence in Data Science for Health Study, Walailak University, Nakhon Si Thammarat 80160, Thailand

DOI:

https://doi.org/10.48048/wjst.2021.9805

Keywords:

Air pollution visualization, Air pollution management, Advection-diffusion equation, Navier-Stokes equations, Finite element method

Abstract

We study the propagation of pollutants emitted from a single generator such as a factory chimney located between 2 mountains as well as its effects on an observed area such as a village or agricultural land. The problem is formulated as a system of partial differential equations, composed of Navier-Stokes equations and an advection-diffusion equation, and is solved by the finite element method. We visualize the propagation of the pollutants for several variants of the problem depending on the heights of the mountains and investigate their negative effects on the observed area by computing an average concentration of the pollutants over the observed area. We found that the observed area between the two mountains experienced a long-term negative effect compared with those located on flat land. This is because the mountain on the side, where the wind is blowing, obstructs the wind resulting in air recirculation. In contrast, the other mountain bounces some pollutants back to the observed area, preventing them from leaving the domain. The higher the mountains, the longer the time the pollutants remain in the observed area. If the heights of the mountains encircling the observed area are not equal, the residual remains in the area longer if the taller mountain is on the windward side.

HIGHLIGHTS

Air Visualization of air pollution between two mountains
Air pollution propagation modeling
A system of partial differential equations for air pollution modeling with FEM

GRAPHICAL ABSTRACT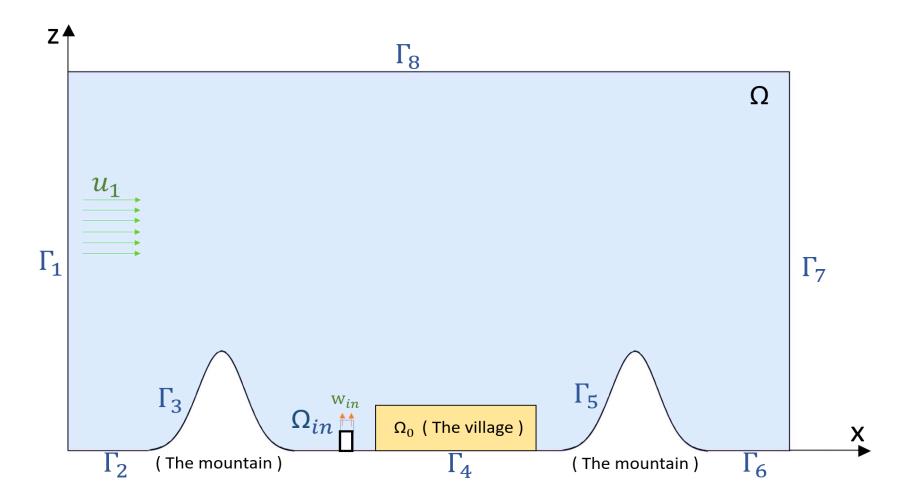

Downloads

Download data is not yet available.

Metrics

Metrics Loading ...

References

M Khafaie, C Yajnik, S Salvi and A Ojha. Critical review of air pollution health effects with special concern on respiratory health. J. Air Pullut. Health 2016; 1, 123-36.

World Health Organization, available at: https://www.who.int, accessed March 2020.

T Roberts, M Unsworth and D Ormrod. Effects of gaseous air pollution in agriculture and horticulture. J. Appl. Ecol. 1983; 20, 704.

JNB Bell and M Treshow. Air pollution and plant life. Wiley, West Sussex, 2003.

J Burney and V Ramanathan. Recent climate and air pollution impacts on Indian agriculture. In: Proceedings of the National Academy of Sciences, Washington DC, 2014, p. 16319-24.

M Ghani, K Gueraoui and S Men-La-Yakhaf. Mathematical modeling and numerical of the atmospheric pollution at the level of free surface. In: Proceedings of the 13th Congrès de Mécanique. Morocco, 2017.

R Temam. The Navier-Stokes equations: theory and numerical analysis. American Mathematical Society Chelsea Publishing, Rhode Island, 2001.

V Girault and PA Raviart. Finite element approximation of the Navier-Stokes equations. Springer-Verlag, Berlin, 2008.

N Pochai. A finite element solution of the mathematical model for smoke dispersion from two sources. Int. J. Math. Comput. Sci. 2011; 5, 1110-4.

KJ Bathe. Finite element procedures. Klaus-Jürgen Bathe, USA, 2014.

JN Reddy. Introduction to the finite element method. McGraw-Hill Education, New York, 2019.

OC Zienkiewicz, RL Taylor and DD Fox. The finite element method. Elsevier Butterworth-Heinemann, Amsterdam, 2014.

Y Hasbani, E Livne and M Bercovier. Finite elements and characteristics applied to advection-diffusion equations. Comput. Fluid. 1983; 11, 71-83.

P Musik and K Jaroensutasine. Two dimensional lattice boltzmann method for cavity flow simulation. Walailak J. Sci. Tech. 2004; 1, 53-70.

M Blatt, A Burchardt, A Dedner, C Engwer, J Fahlke, B Flemisch, C Gersbacher, C Gräser, F Gruber, C Grüninger, D Kempf, R Klöfkorn, T Malkmus, S Müthing, M Nolte, M Piatkowski and O Sander. The distributed and unified numerics environment, version 2.4. Arch. Numer. Software 2016; 4, 13-29.

P Bastian, M Droske, C Engwer, R Klöfkorn, T Neubauer, M Ohlberger and M Rumpf. Towards a unified framework for scientific computing. In: Proceedings of the 15th International Conference on Domain Decomposition Methods. Berlin, Germany, 2005.

C Geuzaine and JF Remacle. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Meth. Eng. 2009; 79, 1309-31.

P Kundu and I Cohen. Fluid mechanics. Elsevier Science, Amsterdam, 2001.

JR Cannon. The one-dimensional heat equation. Cambridge University Press, Cambridge, 2008.

P Bastian, C Engwer, D Göddeke, O Iliev, O Ippisch, M Ohlberger and S Turek. EXA-DUNE: Flexible PDE solvers, numerical methods and applications. In: Proceedings of the European Conference on Parallel Processing. Porto, Portugal, 2014.

F Pasquill. Atmospheric diffusion. Horwood, Chicsester, 1974.

NN Yanenko. The method of fractional steps. Springer-Verlag, Berlin, 1971.

SA Konglok and S Tangmanee. Numerical solution of advection diffusion of an air pollutant by the fractional step method. In: Proceedings of the 3rd National Symposium on Graduate Research, 2002.

S Ulfah, SA Awalludin and Wahidin. Advection-diffusion model for the simulation of air pollution distribution from a point source emission. J. Phys. Conf. Ser. 2018; 948, 12067-75.

P Oyjinda and N Pochai. Numerical simulation of an air pollution model on industrial areas by considering the influence of multiple point sources. Int. J. Diff. Equat. 2019; 2019, 2319831.

S Chomcheon, N Khajohnsaksumeth, B Wiwatanapataphee and X Ge. Modeling and simulation of air pollutant distribution in street canyon area with skytrain stations. Adv. Differ. Equat. 2019; 2019, 459.

Z Zhang, X Xu, L Qiap, D Gong, S Kim, Y Wang and R Mao. Numerical simulations of the effects of regional topography on haze pollution in Beijing. Sci. Rep. 2018; 8, 5504.