Analytical and Numerical Solutions of Vapor Flow in a Flat Plate Heat Pipe

Mohsen GOODARZI; Mohammad Mehdi RASHIDI; Amir BASIRIPARSA

Authors

Mohsen GOODARZI Department of Mechanical Engineering, Faculty of Engineering, Bu-Ali Sina University, Hamedan
Mohammad Mehdi RASHIDI Department of Mechanical Engineering, Faculty of Engineering, Bu-Ali Sina University, Hamedan
Amir BASIRIPARSA Graduate Student of Mechanical Engineering, Islamic Azad University, Hamedan Branch, Young Researchers Club, Hamedan

Keywords:

Differential transform method, flat plate heat pipe, homotopy analysis method, laminar viscous flow

Abstract

In this paper, the optimal homotopy analysis method (OHAM) and differential transform method (DTM) were applied to solve the problem of 2D vapor flow in flat plate heat pipes. The governing partial differential equations for this problem were reduced to a non-linear ordinary differential equation, and then non-dimensional velocity profiles and axial pressure distributions along the entire length of the heat pipe were obtained using homotopy analysis, differential transform, and numerical fourth-order Runge-Kutta methods. The reliability of the two analytical methods was examined by comparing the analytical results with numerical ones. A brief discussion about the advantages of the two applied analytical methods relative to each other is presented. Furthermore, the effects of the Reynolds number and the ratio of condenser to evaporator lengths on the flow variables were discussed.

Graphical abstract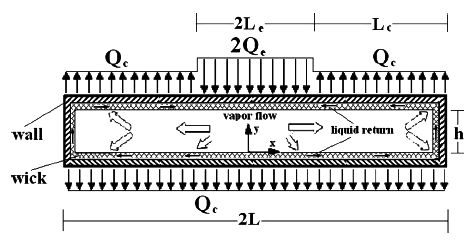

Downloads

Download data is not yet available.

Metrics

Metrics Loading ...

Author Biographies

Mohsen GOODARZI, Department of Mechanical Engineering, Faculty of Engineering, Bu-Ali Sina University, Hamedan

Department of Mechanical Engineering, Faculty of Engineering, Bu-Ali Sina University, Hamedan

Mohammad Mehdi RASHIDI, Department of Mechanical Engineering, Faculty of Engineering, Bu-Ali Sina University, Hamedan

Mohammad Mehdi Rashidi, Ph.D. Associate Professor Bu-Ali Sina University Department of Mechanical Engineering P.O. Box 65175-4161 Hamedan, Iran mm.rashidi@usherbrooke.ca mm_rashidi@yahoo.com Tel.: +98 811 8257409; Fax: +98 811 8257400 http://profs.basu.ac.ir/rashidi/index.php?L=en&pc 1- M.M. Rashidi, H. Shahmohamadi, S. Dinarvand, Analytic Approximate Solutions for Unsteady Two-Dimensional and Axisymmetric Squeezing Flows between Parallel Plates, Mathematical Problems in Engineering, Volume 2008 (2008), Article ID 935095, 13 pages. 2- S. Dinarvand, M.M. Rashidi, A. Doosthoseini, Analytical approximate solutions for two-dimensional viscous flow through expanding or contracting gaps with permeable walls, Central European Journal of Physics 7 (4) (2009). 3- M.M. Rashidi, H. Shahmohamadi, Analytical solution of three-dimensional Navier–Stokes equations for the flow near an infinite rotating disk, Communications in Nonlinear Science and Numerical Simulation 14 (2009) 2999–3006. 4- M.M. Rashidi, G. Domairry, S. Dinarvand, Approximate solutions for the Burger and regularized long wave equations by means of the homotopy analysis method, Communications in Nonlinear Science and Numerical Simulation 14 (2009) 708–717. 5- M.M. Rashidi, D.D. Ganji, S. Dinarvand, Approximate Traveling Wave Solutions of Coupled Whitham-Broer-Kaup Shallow Water Equations by Homotopy Analysis Method, Differential Equations and Nonlinear Mechanics, Volume 2008, Article ID 243459, 8 pages. 6- M.M. Rashidi, D.D. Ganji, S. Dinarvand, Explicit Analytical Solutions of the Generalized Burger and Burger–Fisher Equations by Homotopy Perturbation Method, Numerical Methods for Partial Differential Equations 25 (2) (2009) 409-417. 7- M.M. Rashidi, G. Domairry, S. Dinarvand, The Homotopy Analysis Method for Explicit Analytical Solutions of Jaulent–Miodek Equations, Numerical Methods for Partial Differential Equations 25 (2) (2009) 430-439. 8- M.M. Rashidi, S. Dinarvand, Purely analytic approximate solutions for steady three-dimensional problem of condensation film on inclined rotating disk by homotopy analysis method, Nonlinear Analysis: Real World Applications 10 (2009) 2346–2356. 9- S. Dinarvand, M.M. Rashidi, A reliable treatment of homotopy analysis method for two-dimensional viscous flow in a rectangular domain bounded by two moving porous walls, Nonlinear Analysis: Real World Applications 11 (2010) 1502-1512. 10- M.M. Rashidi, G. Domairry, New Analytical Solution of the Three-Dimensional Navier-Stokes Equations, Modern Physics Letters B 23 (26) (2009) 3147-3155. 11- S. Dinarvand, A. DoostHoseini, E. DoostHoseini, M.M. Rashidi, Series solutions for unsteady laminar MHD flow near forward stagnation point of an impulsively rotating and translating sphere in presence of buoyancy forces, Nonlinear Analysis: Real World Applications 11 (2010) 1159-1169. 12- M.M. Rashidi, E. Erfani, New analytical method for solving Burgers' and nonlinear heat transfer equations and comparison with HAM, Computer Physics Communications 180 (2009) 1539–1544. 13- M.M. Rashidi, The modified differential transform method for solving MHD boundary-layer equations, Computer Physics Communications180 (2009) 2210–2217. 14- M.M. Rashidi, G. Domairry, A. DoostHosseini, S. Dinarvand, Explicit Approximate Solution of the Coupled Kid Equations by using the Homotopy Analysis Method, Int. Journal of Math. Analysis 2 (12) (2008) 581–589. 15- M.M. Rashidi, H. Shahmohamadi, G. Domairry, Variational Iteration Method for Solving Three-Dimensional Navier–Stokes Equations of Flow Between Two Stretchable Disks, Numerical Methods for Partial Differential Equations 27 (2) (2011) 292–301. 16- S. Dinarvand, M.M. Rashidi, H. Shahmohamadi, Analytic approximate solution of three-dimensional Navier–Stokes equations of flow between two stretchable disks, Numerical Methods for Partial Differential Equations 26 (6) (2010) 1594–1607. 17- S. Dinarvand, S. Khosravi, A. Doosthoseini, M.M. Rashidi, The Homotopy Analysis Method for Solving the Sawada–Kotera and Lax’s Fifth-Order KdV Equations, Adv. Theor. Appl. Mech. 1 (7) (2008) 327 – 335. 18- S. Dinarvand, A. Doosthoseini, E. Doosthoseini, M.M. Rashidi, Comparison of HAM and HPM Methods for Berman’s Model of Two-Dimensional Viscous Flow in Porous Channel with Wall Suction or Injection, Adv. Theor. Appl. Mech. 1 (7) (2008) 337 – 347. 19- M.M. Rashidi, M.M. Bastani, NUMERICAL SIMULATION OF AXISYMMETRIC SUPERSONIC VISCOUS FLOW OVER BLUNT CONE BY USING DIAGONAL FOURTH ORDER FINITE DIFFERENCE METHOD, In Persian, Iranian Journal of Engineering Science 19 (10) (1387) (2009) 169-180. 20- M.M. Rashidi, D.D. Ganji, Homotopy Perturbation Combined with Pad´e Approximation for Solving Two Dimensional Viscous Flow in the Extrusion Process, International Journal of Nonlinear Science 7 (4) (2009) 387-394. 21- M.M. Rashidi, S.A. Mohimanian Pour, Analytic Approximate Solutions for Unsteady Boundary-Layer Flow and Heat Transfer due to a Stretching Sheet by Homotopy Analysis Method, Nonlinear Analysis: Modelling and Control 15 (1) (2010) 83–95. …………. 22- M.M. Rashidi, S. Dinarvand, Explicit and Analytical Traveling Wave Solutions of Whitham–Broer–Kaup Shallow Water Equations by homotopy Perturbation Method, International Journal of Non-Linear dynamics and Engineering and Science, (2008). 23- M.M. Rashid, D.D. Ganji, Analytical Solution of Three-Dimensional Navier-Stokes Equations Using HPM-Padé, International Journal of Nonlinear Dynamics in Engineering and Science, In press. 24. M.M. Rashid, M. Keimanesh, Using differential transform method and Padé approximant for solving MHD flow in a laminar liquid film from a horizontal stretching surface, Mathematical Problems in Engineering, Volume 2010 (2010), Article ID 491319, 14 pages. 25. M.M. Rashidi, D.D. Ganji, Homotopy Perturbation Combined with Pad´e Approximation for Solving Two Dimensional Viscous Flow in the Extrusion, International Journal of Nonlinear Science 7 (4) (2009) 387-394. 26. M.M. Rashidi, S.M. Sadri, Solution of the Laminar Viscous Flow in a Semi-Porous Channel in the Presence of a Uniform Magnetic Field by Using the Differential Transform Method, Int. J. Contemp. Math. Sciences 5 (15) (2010) 711–720. 27. H. Shahmohamadi, M.M. Rashidi, A Novel Solution for the Glauert-jet problem by variational iteration method-Padé approximant, Mathematical Problems in Engineering Volume 2010 (2010), Article ID 501476, 7 pages. 28. M.M. Rashidi, E. Erfani, A NOVEL ANALYTICAL METHOD TO INVESTIGATE EFFECT OF RADIATION ON FLOW OF A MAGNETO-MICROPOLAR FLUID PAST A CONTINUOUSLY MOVING PLATE WITH SUCTION AND BLOWING, International Journal of Modeling, Simulation, and Scientific Computing 1 (2010) 219-238. 29. M.M. Rashidi, E. Erfani, Modified differential transform method for solving steady MHD convective and slip flow due to a rotating disk with viscous dissipation and Ohmic heating, International Journal for Computational Methods in Engineering Science & Mechanics, In press. 30. M.M. Rashidi, E. Erfani, Traveling Wave Solutions of WBK Shallow Water Equations by Differential Transform Method, Adv. Theor. Appl. Mech. 3(2010) 6 263 - 271. 31. M.M. Rashidi, S.M. Sadri, New Analytical Solution of Two-Dimensional Viscous Flow in a Rectangular Domain Bounded by Two Moving Porous Walls, International Journal for Computational Methods in Engineering Science & Mechanics 12 (2011) 26–33. 32. M.M. Rashidi, D.D. Ganji and S.M. Sadri, New Analytical Solution of Stagnation Point Flow in a Porous Medium, Journal of Porous Media 14 (12) (2011) 1125–1135. 33. M.M. Rashidi, S.A. Mohimanian Pour, Explicit Solution of Axisymmetric Stagnation Flow Towards a Shrinking Sheet by DTM-Padé, Applied Mathematical Sciences 4 (53) (2010) 2617-2632. 34. M.M. Rashidi, S.A. Mohimanian Pour, A Novel Analytical Solution of Heat Transfer of a Micropolar Fluid through a Porous Medium with Radiation by DTM-Padé, Heat Transfer-Asian Research 39 (8) (2010) 575-589. 35. M.M. Rashidi, N. Laraqi, S.M. Sadri, A Novel Analytical Solution of Mixed Convection about an Inclined Flat Plate Embedded in a Porous Medium Using the DTM-Padé, International Journal of Thermal Sciences 49 (2010) 2405-2412. 36. M.M. Rashidi, E. Erfani, The modified differential transform method for investigating nano boundary-layers over stretching surfaces, International Journal of Numerical Methods for Heat and Fluid Flow 21 (7) (2011) 864-883. 37. M.M. Rashidi and S.A. Mohimanian Pour, Analytic solution of steady three-dimensional problem of condensation film on inclined rotating disk by differential transform method, Mathematical Problems in Engineering, Volume 2010 (2010), Article ID 613230, 15 pages. 38. M.M. Rashidi, S.A. Mohimanian pour, S. Abbasbandy, Analytic Approximate Solutions for Heat Transfer of a Micropolar Fluid through a Porous Medium with Radiation, Communications in Nonlinear Science and Numerical Simulations 16 (2011) 1874–1889. 39. M.M. Rashidi, E. Erfani, A new analytical study of MHD stagnation–point flow in porous media with heat transfer, Computers & Fluids 40 (2011) 172–178. 40. M.M. Rashidi, S.A. Mohimanian Pour, N. Laraqi, A Semi-Analytical Solution of Micro Polar Flow in a Porous Channel with Mass Injection by using Differential Transform Method, NONLINEAR ANALYSIS: MODELLING AND CONTROL 15 (3) (2010) 341–350. 41. E. Erfani, M.M. Rashidi, A. Basiri parsa, The modified Differential Transform Method for solving off-centered stagnation flow towards a rotating disc, International Journal of Computational Methods 7 (4) (2010) 655-670. 42. M.M. Rashidi, S.A. Mohimanian Pour, A novel analytical solution of steady flow over a rotating disk in porous medium with heat transfer by DTM-PADÉ, African Journal of Mathematics and Computer Science Research 3(6) (2010) 93–100. 43. M.M. Rashidi, M. Keimanesh, O. Anwar Bég, T.K. Hung, Magnetohydrodynamic BioRheological Transport Phenomena in a Porous Medium: A simulation of magnetic blood flow control and filtration, International Journal for Numerical Methods in Biomedical Engineering 27 (6) (2011) 805–821. 44. M.M. Rashidi, O. Anwar Bég, A. Habibzadeh, First and second law analysis of an ejector expansion Joule-Thomson cryogenic refrigeration cycle, International Journal of Energy Research, Article first published online: 23 NOV 2010 DOI: 10.1002/er.1800. 45- M.M. Rashidi, N. Laraqi, A. Basiri Parsa, Analytical Modeling of heat convection in magnetized micropolar fluid by using modified differential transform method, Heat Transfer-Asian Research 40 (3) (2011) 187-204. 46- M.M. Rashidi, A.M. Siddiqui, M. Asadi, Application of homotopy analysis method to the unsteady squeezing flow of a second grade fluid between circular plates, Mathematical Problems in Engineering, Volume 2010, Article ID 706840, 18 pages, doi:10.1155/2010/706840. 47- M.M. Rashidi, D.D. Ganji, H. Shahmohamadi, Variational Iteration Method for two-dimensional steady slip flow in micro-channels, Archive of Applied Mechanics 81 (11) (2011) 1597-1605. 48- M. Hamraoui, T. Osman, A. Boucheffa, M.M. Rashidi, Analytical modelling of the threedimensional steady-state temperature in a bearing ring, Mecanique & Industrie 12 (1–4) (2011). 49- M.M. Rashidi, S.A. Mohimanian Pour, Analytic Approximate Solutions for Steady Flow over a Rotating Disk in Porous Medium by Homotopy Analysis Method with Two Auxiliary Parameters, International Journal of Applied Mathematics & Statistics, In press. 50- H. Shahmohamadi, M.M. Rashidi, New Solution for Steady Flow over a Rotating Disk in Porous Medium with Heat Transfer, Progress in Applied Mathematics 1(1) (2011). 51- M.M. Rashidi, N. Rahimzadeh, N. Laraqi, Evaluation of equations of state by using exergy for Air, Nitrogen and Oxygen on throttle reduction efficiency, International Journal of Exergy 9 (3) (2011) 297-318. 52- M.M. Rashidi, T. Hayat, E. Erfani, S.A. Mohimanian Pour, Awatif A-Hendi, Simultaneous effects of partial slip and thermal-diffusion and diffusion-thermo on steady MHD convective flow due to a rotating disk, Communications in Nonlinear Science and Numerical Simulations 16 (2011) 4303–4317. 53- M.M. Rashidi, O. Anwar Bég, M. Asadi, M.T. Rastegari, DTM- Padé Modeling of Natural Convective Boundary Layer Flow of a Nanofluid Past a Vertical Surface, International Journal of Thermal and Environmental Engineering 4 (1) (2012) 13-24. 54- M.M. Rashidi, M.M. Bastani, O. Anwar Bég, Numerical Simulation of Axisymmetric Supersonic Viscous Flow over a Blunt Cone with a Diagonal Fourth Order Finite Difference Method, Proceedings of the Institution of Mechanical Engineers, Part G, Journal of Aerospace Engineering, Published online before print November 11, 2011, doi:10.1177/0954410011408303. 55- M.M. Rashidi, E. Erfani, Analytical method for solving steady MHD convective and slip flow due to a rotating disk with viscous dissipation and Ohmic heating, Engineering Computations, In press. 56- M.M. Rashidi, O. Anwar Bég, A. Basiri Parsa, F. Nazari, Analysis and optimization of a transcritical power cycle with regenerator using artificial neural networks and genetic algorithms, PROC. IMECHE - PART A: J. POWER AND ENERGY 225 (6) (2011) 701-717. 57- M.M. Rashidi, M. Keimanesh, S.C. Rajvanshi, Study of Pulsatile flow in a porous annulus with the homotopy analysis method, International Journal of Numerical Methods for Heat and Fluid Flow, In press. 58- M.M. Rashidi, D.D. Ganji, Homotopy perturbation method for solving flow in the extrusion processes, Iranian Journal of Engineering Science 23 (3&4) (2010) 267-272. 59- N. Laraqi, M.M. Rashidi, J.M. Garcia de Maria, A. Baïri, Analytical model for the thermo-hydrodynamic behaviour of a thin lubricant film, Tribology International 44 (2011) 1083–1086. 60- M.M. Rashidi, T. Hayat, A. Basiri parsa, Solving of boundary-layer equations with transpiration effects, governance on a vertical permeable cylinder using modified differential transform method, Heat Transfer-Asian Research 40 (8) (2011) 677–692. 61- M.M. Rashidi, O. Anwar Bég, N. Rahimzadeh, A generalized Differential Transform Method for combined free and forced convection flow about inclined surfaces in porous media, Chemical Engineering Communications 199 (2) (2011) 257-282. 62- M.M. Rashidi, O. Anwar Bég, M.T. Rastegari, A study of non-Newtonian flow and heat transfer over a non-isothermal wedge using the Homotopy Analysis Method, Chemical Engineering Communications 199 (2) (2011) 231-256. 63- M.M. Rashidi, Ali J. Chamkha, M. Keimanesh, Application of multi-step differential transform method on flow of a second-grade fluid over a stretching or shrinking sheet, American Journal of Computational Mathematics 1 (2) (2011) 119-128. 64- A. Basiri parsa, M.M. Rashidi, O. Anwar Bég and M. Asadi, Approximate Explicit Solutions of Steady Similar Sakiadis Boundary-Layer Flows with the Homotopy Analysis Method, Advances in Applied Science Research, In press. 65- M.M. Rashidi, N. Galanis, F. Nazari, A. Basiri Parsa, L. Shamekhi, Parametric Analysis and Optimization of Regenerative Clausius and Organic Rankine Cycles with Two Feedwater Heaters Using Artificial Bees Colony and Artificial Neural Network, Energy 36 (2011) 5728-574. 66- O. Anwar Bég, M.M. Rashidi, T.A. Bég, M. Asadi, Homotopy Analysis of Transient Magneto-Bio-Fluid Dynamics of Micropolar Squeeze Film in a Porous Medium: A Model for Magneto-Bio-Rheological Lubrication, Journal of Mechanics in Medicine and Biology, DOI No: 10.1142/S0219519411004642 Accepted 2011-07-12. 67- M. Keimanesh, M.M. Rashidi, Ali J. Chamkha, R. Jafari, Study of a third grade non-Newtonian fluid flow between two parallel plates using the Multi-step differential transform method, Computers and Mathematics with Applications 62 (2011) 2871–2891. 68- M.M. Rashidi, S.A. Mohimanian Pour, T. Hayat, S. Obaidat, Analytic Approximate Solutions for Steady Flow over a Rotating Disk in Porous Medium with Heat Transfer by Homotopy Analysis Method, Computers and Fluids 54 (2012) 1–9. 69- M. Ferdows, Md. Jashim Uddin, M.M. Rashidi, N. Rahimzadeh, Numerical Analysis of Mixed Convection over Horizontal Moving Porous Flat Plate by the Method of One Parameter Continuous Group Theory, International Journal of Numerical Methods for Heat and Fluid Flow, In press. 70- M.M. Rashidi, T. Hayat, M. Keimanesh , A.A. Hendi, New analytical method for the study of natural convection flow of a non-Newtonian, International Journal of Numerical Methods for Heat and Fluid Flow, In press. 71- H. Shahmohamadi, M.M. Rashidi, Explicit Solutions for Steady Three-Dimensional Problem of Condensation Film on Inclined Rotating Disk, International Journal of Fluid Mechanics Research 38 (5.30) (2011) 424-436. 72- M.M. Rashidi, M. Keimanesh, S.C. Rajvanshi, S. Wasu, Pulsatile flow through annular space bounded by outer porous cylinder and an inner cylinder of permeable material, International Journal for Computational Methods in Engineering Science & Mechanics, In press. 73- M.M. Rashidi T. Hayat and A. Basiri parsa, MHD boundary-layer fow over a stretching surface with internal heat generation or absorption, International Journal of Applied Mathematics & Statistics, In press. 74- M.M. Rashidi, E. Erfani, O. Anwar Bég, S.K. Ghosh, Modified Differential Transform Method (DTM) Simulation of Hydromagnetic Multi-Physical Flow Phenomena from a Rotating Disk, World Journal of Mechanics 1 (2011) 217-230. 75- M.M. Rashidi, A.M. Siddiqui, M.T. Rastegari, Analytical Solution of Squeezing Flow between Two Circular Plates, International Journal for Computational Methods in Engineering Science & Mechanics, In press. 76- M.M. Rashidi, Group theory and differential transform analysis of mixed convective heat and mass transfer from a horizontal surface with chemical reaction effects, Chemical Engineering Communications, In press. 77- T. A. Bég, M.M. Rashidi, O. Anwar Bég, N. Rahimzadeh, Differential transform semi-numerical analysis of biofluid-particle suspension flow and heat transfer in non-Darcian porous mediad, Computer Methods in Biomechanics and Biomedical Engineering, In press. 78- O. Anwar Bég, M.M. Rashidi, A. Aziz and M. Keimanesh, DIFFERENTIAL TRANSFORM STUDY OF HYPERSONIC LAMINAR BOUNDARY LAYER AERODYNAMIC FLOW AND HEAT TRANSFER OVER SLENDER AXISYMMETRIC BODIES OF REVOLUTION, International Journal of Applied Mathematics and Mechanics, In press. 79- H. Shahmohamadi, M. M. Rashidi and O. Anwar Bég, A NEW TECHNIQUE FOR SOLVING STEADY FLOW AND HEAT TRANSFER FROM A ROTATING DISK IN HIGH PERMEABILITY MEDIA, International Journal of Applied Mathematics and Mechanics, In press.

Amir BASIRIPARSA, Graduate Student of Mechanical Engineering, Islamic Azad University, Hamedan Branch, Young Researchers Club, Hamedan

Graduate Student of Mechanical Engineering, Islamic Azad University, Hamedan Branch, Young Researchers Club, Hamedan

References

A Basiulis, H Tanzer and S McCabe. Thermal management of high power PWB’s through the use of heat pipe substrates. In: Proceedings of the 6th Annual International Electronics Packaging Conference, San Diego, California. 1986, p. 501.

MJ Rightley, CP Tigges, RC Givler, CV Robino, JJ Mulhall and PM Smith. Innovative wick design for multi-source flat plate heat pipes. Microelectron. J. 2003; 34, 187-94.

M Thomson, C Ruel and M Donato. Characterization of a flat plate heat pipe for electronic cooling in a space environment. In: Proceedings of the 1989 National Heat Transfer Conference, Heat Transfer in Electronics, Philadelphia, Pennsylvania. 1989, p. 59-65.

H Ooijen and CJ Hoogendoorn. Vapor flow calculations in a flat-plate heat pipe. AIAA J. 1979; 17, 1251-9.

K Vafai, N Zhu and W Wang. Analysis of flow and heat transfer characteristics of an asymmetrical flat plate heat pipe. Int. J. Heat Mass Tran. 1992; 35, 2087-99.

K Vafai, N Zhu and W Wang. Analysis of asymmetrical disk-shaped and flat-plate heat pipes. ASME J. Heat Tran. 1995; 117, 209-18.

N Zhu and K Vafai. Vapor and liquid flow in an asymmetrical flat plate heat pipe: a three dimensional analytical and numerical investigation. Int. J. Heat Mass Tran. 1998; 41, 159-74.

N Zhu and K Vafai. Analytical modeling of the startup characteristics of asymmetrical flat plate and disk-shaped heat pipes. Int. J. Heat Mass Tran. 1998; 41, 2619-37.

Y Wang and K Vafai. Transient characterization of flat plate heat pipes during startup and shutdown operations. Int. J. Heat Mass Tran. 2000; 43, 2641-55.

EK Levy. Theoretical investigation of heat pipes operating at low vapor pressures. J. Eng. Ind. 1968; 90, 547-52.

YM Brovalsky, PI Bystrov and MV Melkinov. The method of calculation and investigation of high temperature heat pipe characteristics taking into account the vapor flow compressibility, friction, and velocity profile. In: Proceedings of the 2nd International Heat Pipe Conference, Bologna, Italy. 1976, p. 113-22.

A Faghri. Performance characteristics of a concentric annular heat pipe: part II-vapor flow analysis. ASME J. Heat Tran. 1989; 111, 851-7.

JH Jang. 1988, An Analysis of Startup from the Frozen State and Transient Performance of Heat Pipes, Ph. D. Dissertation. Georgia Institute of Technology, USA.

Y Cao, A Faghri and ET Mahefkey. The thermal performance of heat pipes with localized heat input. Int. J. Heat Mass Tran. 1989; 32, 1279-87.

N Zhu and K Vafai. The effects of liquid vapor coupling and non-Darcian transport on asymmetrical diskshaped heat pipes. Int. J. Heat Mass Tran. 1996; 39, 2095-113.

MT North and CT Avedisian. Heat pipe for cooling high flux/high power semiconductor chips. J. Electro. Packag. 1993; 115, 112-7.

N Zhu and K Vafai. Numerical and analytical investigation of vapor flow in a disk-shaped heat pipe incorporating secondary flow. Int. J. Heat Mass Tran. 1997; 40, 2887-900.

YS Chen, KH Chien, CC Wang, TC Hung and BS Pei. A Simplified transient three-dimensional model for estimating the thermal performance of the vapor chambers. Appl. Therm. Eng. 2006; 26, 2087-94.

Y Xuan, Y Hong and Q Li. Investigation on transient behaviors of flat plate heat pipes. Exp. Therm. Fluid Sci. 2004; 28, 249-55.

R Sonan, S Harmand, J Pellé, D Leger and M Fakès. Transient thermal and hydrodynamics model of flat heat pipe for the cooling of electronics components. Int. J. Heat Mass Tran. 2008; 51, 6006-17.

Y Koito, H Imura, M Mochizuki, Y Saito and S Torii. Numerical analysis and experimental verification on thermal fluid phenomena in vapor chamber. Appl. Therm. Eng. 2006; 26, 1669-76.

R Boukhanouf, A Haddad, MT North and C Buffone. Experimental investigation of a flat plate heat pipe performance using IR thermal imaging camera. Appl. Therm. Eng. 2006; 26, 2148-56.

AH Nayfeh. Perturbation Methods. Wiley, New York, 2000.

SJ Liao. 1992, The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, Ph. D. Thesis: Shanghai Jiao Tong University, China.

SJ Liao. Beyond Perturbation: Introduction to the Homotopy Analysis Method. Chapman & Hall/CRC Press, Boca Raton, 2003.

G Domairry and M Fazeli. Homotopy analysis method to determine the fin efficiency of convective straight fins with temperature dependent thermal conductivity. Commun. Nonlinear Sci. Numer. Simul. 2009; 14, 489-99.

MM Rashidi, G Domairry and S Dinarvand. Approximate solutions for the Burger and regularized long wave equations by means of the Homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009; 14, 708-17.

Z Ziabakhsh, G Domairry and M Esmaeilpour. Solution of the laminar viscous flow in a semi-porous channel in the presence of a uniform magnetic field by using the Homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009; 14, 1284-94.

MM Rashidi and S Dinarvand. Purely analytic approximate solutions for steady three-dimensional problem of condensation film on inclined rotating disk by Homotopy analysis method. Nonlinear Anal. R. World Appl. 2009; 10, 2346-56.

Z Ziabakhsh and G Domairry. Analytic solution of natural convection flow of a non-Newtonian fluid between two vertical flat plates using Homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009; 14, 1868-80.

JH He. Homotopy perturbation technique. Comput. Meth. Appl. Mech. Eng. 1999; 178, 257-62.

JK Zhou. Differential Transformation and Its Applications for Eelectrical Circuits. Huazhong University Press, Wuhan, China, 1986.

CK Chen and SH Ho. Solving partial differential equations by two dimensional differential transform method. Appl. Math. Comput. 1999; 106, 171-9.

F Ayaz. Solutions of the systems of differential equations by differential transform method. Appl. Math. Comput. 2004; 147, 547-67.

IH Abdel-Halim Hassan. Comparison differential transformation technique with Adomain decomposition method for linear and nonlinear initial value problems. Chaos Solitons & Fractals 2008; 36, 53-65.

A Arikoglu and I Ozkol. Solution of differential-difference equations by using differential transform method. Int. J. Appl. Math. Comput. 2006; 181, 154.